
Наиболее часто тренд представляется линейной зависимостью исследуемой величины вида
![]() где y – исследуемая переменная (например, производительность) или зависимая переменная;
где y – исследуемая переменная (например, производительность) или зависимая переменная;
x – число, определяющее позицию (второй, третий и т.д.) года в периоде прогнозирования или независимая переменная.
При линейной аппроксимации связи между двумя параметрами для нахождения эмпирических коэффициентов линейной функции используется наиболее часто метод наименьших квадратов. Суть метода состоит в том, что линейная функция «наилучшего соответствия» проходит через точки графика, соответствующие минимуму суммы квадратов отклонений измеряемого параметра. Такое условие имеет вид:
где n – объем исследуемой совокупности (число единиц наблюдений).

Рис. 5.3. Построение тренда методом наименьших квадратов
Значения констант b и a или коэффициента при переменной Х и свободного члена уравнения определяются по формуле:

В табл. 5.1 приведен пример вычисления линейного тренда по данным [1].
Таблица 5.1. Вычисление линейного тренда

Методы сглаживания колебаний.
При сильных расхождениях между соседними значениями тренд, полученный методом регрессии, трудно поддается анализу. При прогнозировании, когда ряд содержит данные с большим разбросом колебаний соседних значений, следует их сгладить по определенным правилам, а потом искать смысл в прогнозе. К методу сглаживания колебаний
относят: метод скользящих средних (рассчитывается n-точечное среднее), метод экспоненциального сглаживания. Рассмотрим их.
Метод «скользящих средних» (МСС).
МСС позволяет сгладить ряд значений с тем, чтобы выделить тренд. При использовании этого метода берется среднее (обычно среднеарифметическое) фиксированного числа значений. Например, трехточечное скользящее среднее. Берется первая тройка значений, составленная из данных за январь, февраль и март (10 + 12 + 13), и определяется среднее, равное 35 : 3 = 11,67.
Полученное значение 11,67 ставится в центре диапазона, т.е. по строке февраля. Затем «скользим на один месяц» и берется вторая тройка чисел, начиная с февраля по апрель (12 + 13 + 16), и рассчитывается среднее, равное 41 : 3 = 13,67, и таким приемом обрабатываем данные по всему ряду. Полученные средние представляют новый ряд данных для построения тренда и его аппроксимации. Чем больше берется точек для вычисления скользящей средней, тем сильнее происходит сглаживание колебаний. Пример из МВА построения тренда дан в табл. 5.2 и на рис. 5.4.
Таблица 5.2 Расчет тренда методом трехточечного скользящего среднего

Характер колебаний исходных данных и данных, полученных методом скользящего среднего, иллюстрирован на рис. 5.4. Из сравнения графиков рядов исходных значений (ряд 3) и трехточечных скользящих средних (ряд 4), видно, что колебания удается сгладить. Чем большее число точек будет вовлекаться в диапазон вычисления скользящей средней, тем нагляднее будет вырисовываться тренд (ряд 1). Но процедура укрупнения диапазона приводит к сокращению числа конечных значений и это снижает точность прогноза.
Прогнозы следует делать исходя из оценок линии регрессии, составленной по значениям исходных данных или скользящих средних.

Рис. 5.4. Характер изменения объема продаж по месяцам года:
исходные данные (ряд 3); скользящие средние (ряд 4); экспоненциальное сглаживание (ряд 2); тренд, построенный методом регрессии (ряд 1)
Метод экспоненциального сглаживания.
Альтернативный подход к сокращению разброса значений ряда состоит в использовании метода экспоненциального сглаживания. Метод получил название «экспоненциальное сглаживание» в связи с тем, что каждое значение периодов, уходящих в прошлое, уменьшается на множитель (1 – α).
Каждое сглаженное значение рассчитывается по формуле вида:
St =aYt +(1−α)St−1,
где St – текущее сглаженное значение;
Yt – текущее значение временного ряда; St – 1 – предыдущее сглаженное значение; α – сглаживающая константа, 0 ≤ α ≤ 1.
Чем меньше значение константы α , тем менее оно чувствительно к изменениям тренда в данном временном ряду.

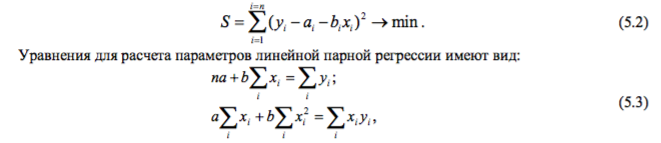
Привести пример расчета для экспоненицального сглаживания не хватило мозгов?
Большое Вам спасибо за расчет линейной зависимости!